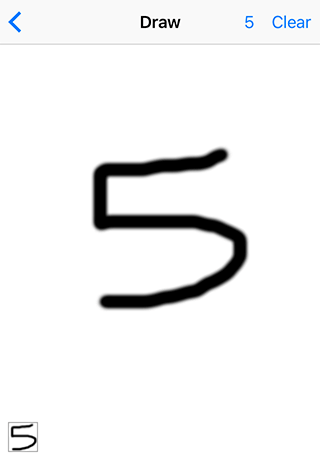Convolutional Networks: from TensorFlow to iOS BNNS
MNIST digit recognition quest.
A hero
BNNS - basic neural network subroutines - is a new library in iOS 10 and macOS 10.12.
With BNNS you can run inference in neural nets, using pre-trained model. As of now, training is not supported, and types of nets you could build are limited to convolution, pooling and fully connected layers, with a limited set of activation functions.
BNNS is CPU optimized. A GPU counterpart was added to Metal Performance Shaders.
Read more:
A noble quest
Let’s make a digit recognizer based on MNIST database of handwritten digits:
Convolutional network is a good fit for this task.
(image credit: The Asimov Institute)
We are going to use TensorFlow tutorial to train a pretty confident model!
I’ve included pre-trained model in the repository for you, but here is the full TensorFlow script from the tutorial to generate the model: mnist-nn.ipynb (might take a couple of hours to train).
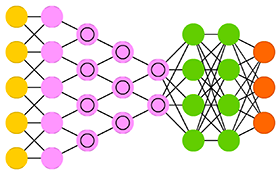
Here is an overview of this neural network, with a focus on data transformation (I’m not showing activation and bias here):
- It takes a 28 by 28 image
- convolves it with a 5x5 32 channel kernel, to produce 28x28 32 channel data
- reduces data with max pool 2x2 kernel, to produce 14x14 32 channel data
- convolves it with 5x5 64 channel kernel, to produce 14x14 64 channel data
- reduces data with max pool 2x2 kernel, to produce 7x7 64 channel data
- reshapes data as a vector of 3136 values
- multiplies with a matrix, to produce vector of 1024 values
- multiples with a matrix, to produce vector of 10 values
Somewhat magically, the last 10 values give probability to each of 10 possible digits. We take the one with maximum probability.
The script writes these model files (weights and bias for convolution and fully connected mul layers):
- conv1:
model-h1w-5x5x1x32,model-h1b-32 - conv2:
model-h2w-5x5x32x64,model-h2b-64 - mul1:
model-h3w-3136x1024,model-h3b-1024 - mul2:
model-h4w-1024x10,model-h4b-10
It’s dangerous to go alone! Take this
Before we jump to importing the model into iOS app, let me warn you that BNNS API is somewhat verbose:
let weights_data = BNNSLayerData(data: weights, data_type: BNNSDataTypeFloat32, data_scale: 0, data_bias: 0, data_table: nil)
let bias_data = BNNSLayerData(data: bias, data_type: BNNSDataTypeFloat32, data_scale: 0, data_bias: 0, data_table: nil)
let activ = BNNSActivation(function: BNNSActivationFunctionRectifiedLinear, alpha: 0, beta: 0)
var layerParams = BNNSConvolutionLayerParameters(x_stride: 1, y_stride: 1, x_padding: 2, y_padding: 2,
k_width: 5, k_height: 5, in_channels: 1, out_channels: 32,
weights: weights_data, bias: bias_data, activation: activ)
...
Let’s hide this boilerplate, so we can express ourselves in clear:
let nn = BnnsBuilder()
.shape(width: 28, height: 28, channels: 1)
.kernel(width: 5, height: 5)
.convolve(weights: weights[0], bias: weights[1])
.shape(width: 28, height: 28, channels: 32)
.maxpool(width: 2, height: 2)
.shape(width: 14, height: 14, channels: 32)
.convolve(weights: weights[2], bias: weights[3])
.shape(width: 14, height: 14, channels: 64)
.maxpool(width: 2, height: 2)
.shape(width: 7, height: 7, channels: 64)
.connect(weights: weights[4], bias: weights[5])
.shape(size: 1024)
.connect(weights: weights[6], bias: weights[7])
.shape(size: 10)
.build()!
This is the whole network. Note how data shape is explicitly declared between layers.
The BnnsBuilder is in this file: BnnsBuilder.swift.
There is a bug in BNNSFilterCreateConvolutionLayer crashing on nil for filter_params, and I couldn’t make an empty BNNSFilterParameters in Swift, so this is where BnnsHelper.h kicks in. If you can make it a single Swift file, please let me know.
A challenge
Are we all set to import the model into our BNNS network? Not so fast.
You might have noticed cryptic transforms at the end of training script:
model[0].transpose([3,2,0,1])
model[2].transpose([3,2,0,1])
model[4].reshape([7,7,64,1024]).transpose([3,2,0,1])
model[6].transpose()
This is dark magic of data aligning.
BNNS accepts continuous one-dimensional arrays of data, and declares how it will interpret them as multidimensional matrices. We are to abide to BNNS rules when exporting data from TensorFlow.
Basically, BNNS declares that it will read data row by row, by input channels, by output channels.
For example, with a 3x2x2 matrix (3 rows, 2 columns, 2 channels):
a[:,:,0]
# array([[1, 2],
# [3, 4],
# [5, 6]])
a[:,:,1]
# array([[ 7, 8],
# [ 9, 10],
# [11, 12]])
BNNS would expect it to be flattened as [1,2,3,4,5,6,7,8,9,10,11,12]
On the other hand, when we do numpy.ravel in TensorFlow, this happens:
a.ravel()
# array([ 1, 7, 2, 8, 3, 9, 4, 10, 5, 11, 6, 12])
numpy.ravel iterates each dimension in order, starting from the last one. Parameter order='F' would reverse dimensions, but it’s still not what we need. We have to explicitly reshuffle dimensions so that ravel will produce flattened array as BNNS expects it:
a.transpose([2,0,1]).ravel()
# array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
We need these transformations for the multidimensional weights data. Bias data is one-dimensional, with nothing to worry about.
I have another script for you that loads model files back into TensorFlow: mnist-predict-from-model.ipynb, reversing these transformations.
Hack’n’slash
Courage! Finally, we have neural network in BNNS, the model is ready, and we are ready to pack everything in a beautiful app. Which I did for you here:
The app loads test data from MNIST (not the train data we trained our model on) – there are 10,000 images to recognize.
There are two modes of operation: pick images to recognize one by one, or recognize the whole page.
Again, I hide BNNS boilerplate under simple BnnsNetwork facade – running the network is as simple as
let outputs = nn.apply(input: imageData)
return outputs.index(of: outputs.max()!)!
Update: now you can conjure digits:
For proper recognition, I’m recreating MNIST preprocessing “by computing the center of mass of the pixels, and translating the image so as to position this point at the center of the 28x28 field”.
Treasure!
Among incorrectly recognized digits there is this couple:

The left one is definitely 8, incorrectly recognized as 2.
The right one is labeled as 2, but recognized as 7. I would argue that this is 7 indeed.
Interesting MNIST bug: human transcribers sometimes changed label to match perceived digit. Here are 3 in train set. pic.twitter.com/Q9AO1yDudY
— tom white (@dribnet) February 7, 2016
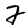
What do you think?
The End
Source code: paiv/mnist-bnns